My research focuses on the physics of "granular materials"—collections of particles larger than tens of micrometers. This includes everyday materials like sand, food products, and pharmaceuticals. Unlike smaller particles governed by thermal motion, these "a-thermal" systems do not reach equilibrium, and their physics is largely unresolved. My primary goal is to understand their "rheology," which I define broadly as any phenomenon involving their motion, including properties like flowability, stiffness, and mixing.
To tackle this complexity, I investigate fundamental behaviors in relatively simple systems, often under shear or vibration. I believe that understanding these basics is the key to unlocking more complex phenomena. My work has applications in engineering and geophysics, leading to related projects on concrete and landslide dynamics.
My approach is methodologically flexible. I draw upon theory (statistical and continuum mechanics), numerical simulation (primarily the Discrete Element Method), and experiment. For each research question, I select the most fitting approach, and I am currently developing new experimental setups and skills in the Katsuragi Laboratory at Osaka University.

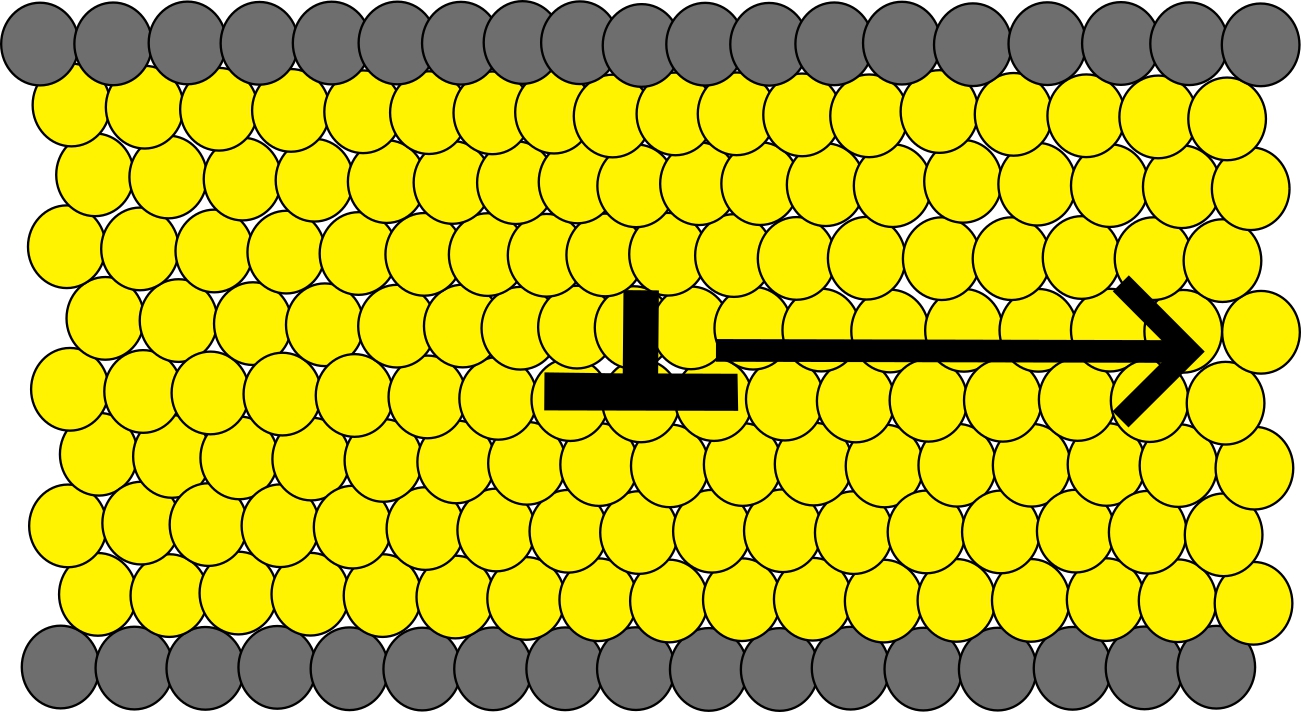
The rheology of granular materials changes dramatically based on how their particles are arranged. For instance, structures like arches and cobblestones derive their strength from a clever arrangement of particles. While this link between structure and strength is vital for engineering, the underlying physics is not yet well understood. It was widely believed that crystalline (regularly arranged) granular materials were stronger than randomly packed ones. However, I discovered that introducing a single lattice defect, known as a 'dislocation,' into a granular crystal dramatically decreases its strength—making it even weaker than a random structure. This finding was achieved by applying the Peierls stress theory, a concept originally from metal and semiconductor physics, to the world of granular materials.

When a granular system contains a mix of particles with varying sizes, masses, or shapes, it often exhibits segregation—a phenomenon where similar particles cluster together under flow. This is especially true for differences in size, where particle size segregation becomes a major issue in industrial processes. In my research, I discovered a fascinating phenomenon. When I vibrate a mix of large and small particles in a confined, flat container, they segregate if there are only a few small particles. However, if I increase the number of small particles, the segregation disappears. I am continuing this research to uncover the fundamental physical mechanism that drives this behavior.

Typically, the diffusivity of the center of mass of a particle decreases as the matrix density increases. However, rod diffusivity can exhibit the opposite behavior in certain matrices. This phenomenon has been explained using various fuzzy concepts such as dynamic correlations, geometrical constraints, confinements, or dynamic arrests. We have found that the increase in the diffusion coefficient can even occur in simple Markovian process and have explained the increases in rod diffusivity based on the Markovian nature.
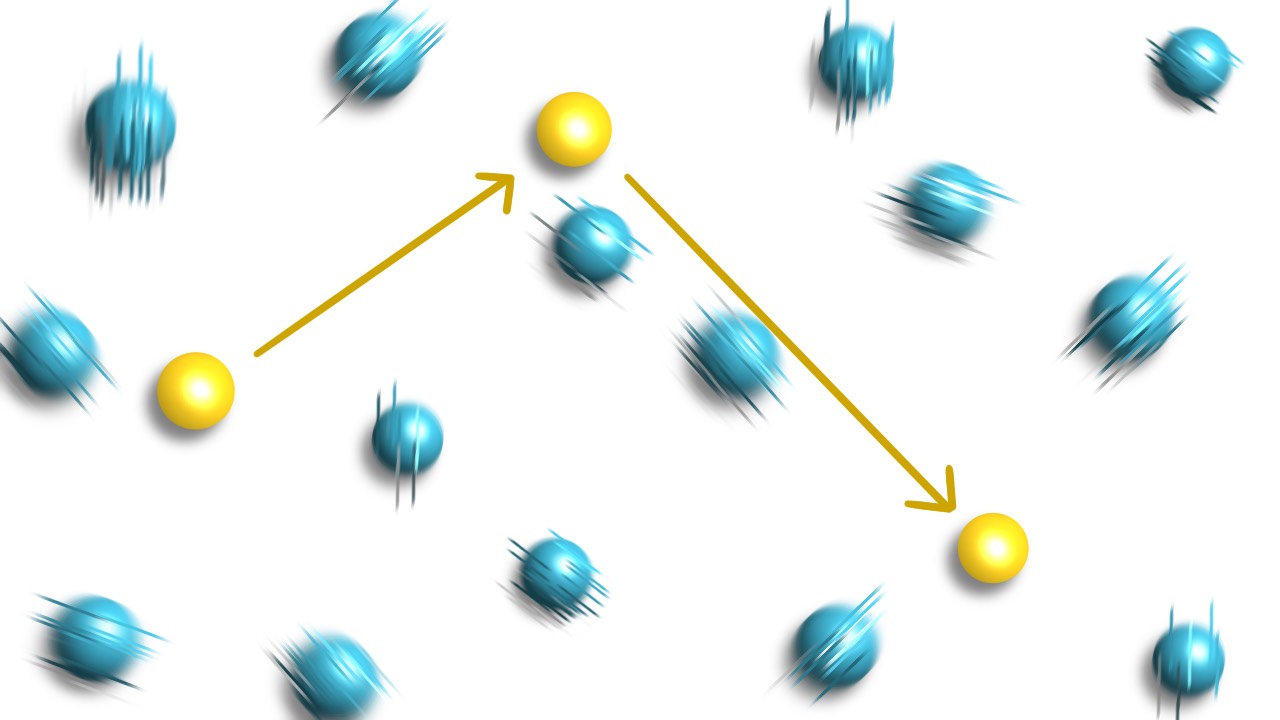
Recently, a type of diffusion called "Brownian yet non-Gaussian diffusion" has been observed. This phenomenon can be explained by the concept of "fluctuating diffusivity," where the diffusion coefficient of a particle varies over time. There are two known origins for fluctuating diffusivity: heterogeneous spatial/temporal environments and conformational fluctuations. However, we have proposed a third novel origin for fluctuating diffusivity in the study of simple binary gas mixtures, which we have studied numerically.
I studied the dynamics of a single tracer particle in an ideal gas and found that it exhibits various interesting behaviors, even in its simple nature. For example, the mean square displacement of the tracer particle has a plateau, and strong non-Gaussian diffusion occurs in certain parameter regimes.