粉体は,粒径数十マイクロメートル以上の粒子の集合体を指します. 私たちの身の回りに粉体は溢れています. 例えば,土,砂,火山灰,花粉,化粧品パウダー,粉薬,小麦粉,コーヒー豆,塩,パチンコ球など挙げたらキリがありません. 仲井はこれら粉体のレオロジーの研究をしています. レオロジーとは,狭義には物質の変形と応答を理解する学問ですが, 仲井は何かが動けばレオロジーの範疇と考えます. 様々な粉体のレオロジー特性(硬さ,流れやすさ,壊れやすさ,混ざりやすさ,動きやすさ)の基礎研究に取り組んでいます.
粉体は古くから人間生活と深く関わり,経験的な知識によって利用・制御されてきました. しかし,その本質的な理解はいまだ十分とは言えず,基礎物理の観点からの研究が強く求められています. 例えば,次のような身近な現象でさえ,さまざまな仮説や経験則が知られていますが, 物理的なメカニズムは十分には理解されていません.
粉体のレオロジーを統一的に記述する枠組みは,いまだ完成していません. 粒子が離散的な性質(粒々性)をもつため,流体力学や弾性体力学では, 多くの場合,その振る舞いを適切に記述することができません. また,多体問題ではあるものの,熱平衡系ではないため, 通常の統計力学を直接適用することも困難です. このように,身近でありながら未解決な問題を多く含む粉体に対して, 仲井はさまざまなシンプルな設定を考えて研究を進めることが多いです.
研究手法はできるだけ縛らない方針とし,対象や目的,資金面や研究環境に応じて, 適切な手法を選択/習得しながら研究を進めています. 理論的研究としては,(広義の)統計力学や(広義の)連続体力学を扱うことが多いです. 数値計算では,主に離散要素法(Discrete Element Method)を用い,必要に応じてスーパーコンピュータも利用します. 実験研究も展開しており,簡易なセンサーやアクチュエータを組み合わせたテーブルトップ実験装置の構築にも取り組んでいます.

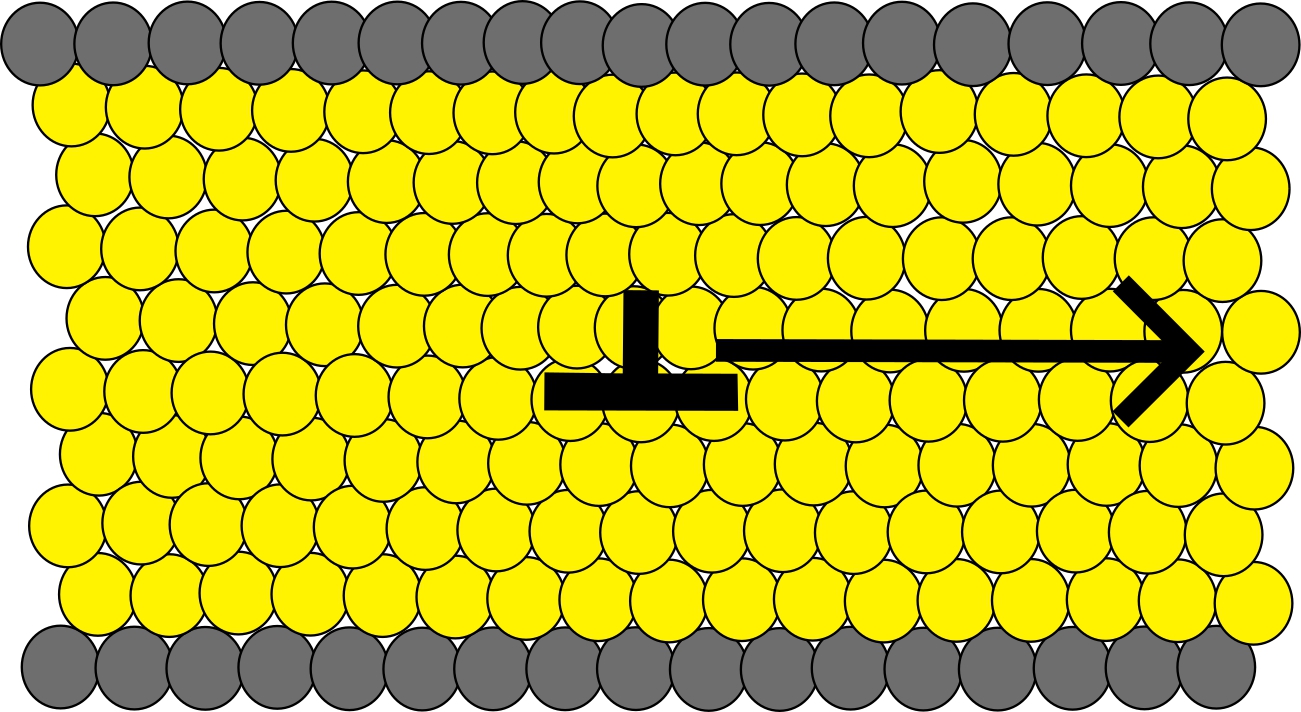
粉体のレオロジー特性は,その粒子配列構造に応じて劇的に変化します. 例えばアーチ/城壁/石畳は,粒子(石)を巧みに配置することで強固な構造を実現したものです. この構造と強度の関係は工学的に重要である一方,物理的な基礎知見は乏しいのが現状です. 従来,粉体を周期的/規則的に配列させると, ランダムな構造よりも強度が増すことは知られていました. これに対し仲井は,その規則構造中に”転位”と呼ばれる格子欠陥を導入すると, 強度が(ランダム構造と比べても)”劇的に”低下することを発見しました. この発見は,金属や半導体結晶で知られるPeierls応力理論を粉体系へ応用することで見出すことができました.

粉体系は,大きさ,質量,形状等にバラ付きがあると, 流動下で類似粒子が凝集する現象がしばしば生じます. 特に,粒子のサイズ違いにより生じる粒度偏析は,工学上問題になります. 仲井は,平たい領域に大小粒子を閉じ込めて振動すると, 小粒子が少ない場合は偏析し,小粒子が多いと偏析が解消する現象を発見しました. 偏析現象の物理機構解明を目指し研究を続けています.
線形粘弾性の研究.準備中
加振粉体の研究,準備中
粒径数マイクロメートル以下の粒子はランダムに動きます(ブラウン運動). マクロな系の流れやすさは,ミクロに見れば全て粒子の動きやすさによって決まっています. 粒子の動きやすさは,粒子の性質と周囲環境双方に依存します. 仲井は,粒子の質量,形状,環境が粒子の動きやすさにどう影響するのかをシンプルな系を考えて研究していました.
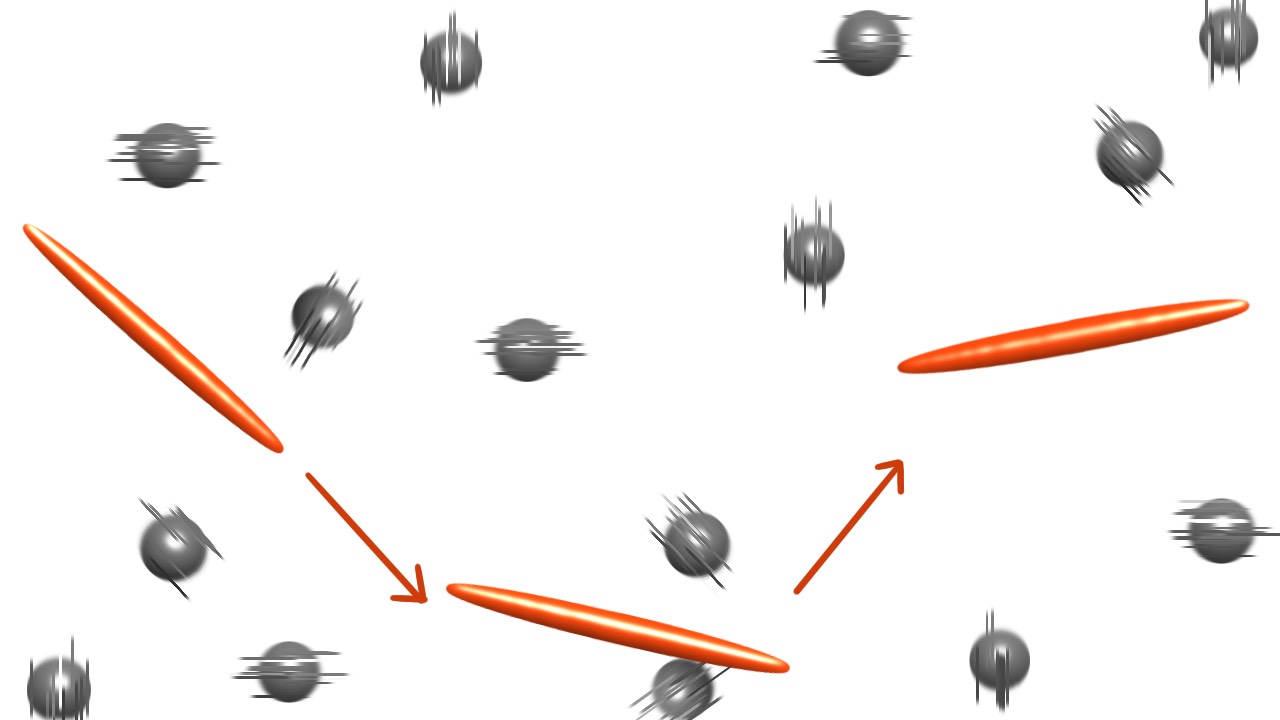
粒子の運動性は粒子形状に強く依存します. 過去の理論研究で,非常に細長い粒子集合体は,濃度が濃くなる程運動性が増すという, ちょっと直感とはズレた挙動が生じることが知られていました. 現象の正確な理解は乏しい状況でしたが,仲井は,力学的に妥当かつシンプルなモデルを構築することで, 濃度増加に伴う運動性増加の機構を解明しました.
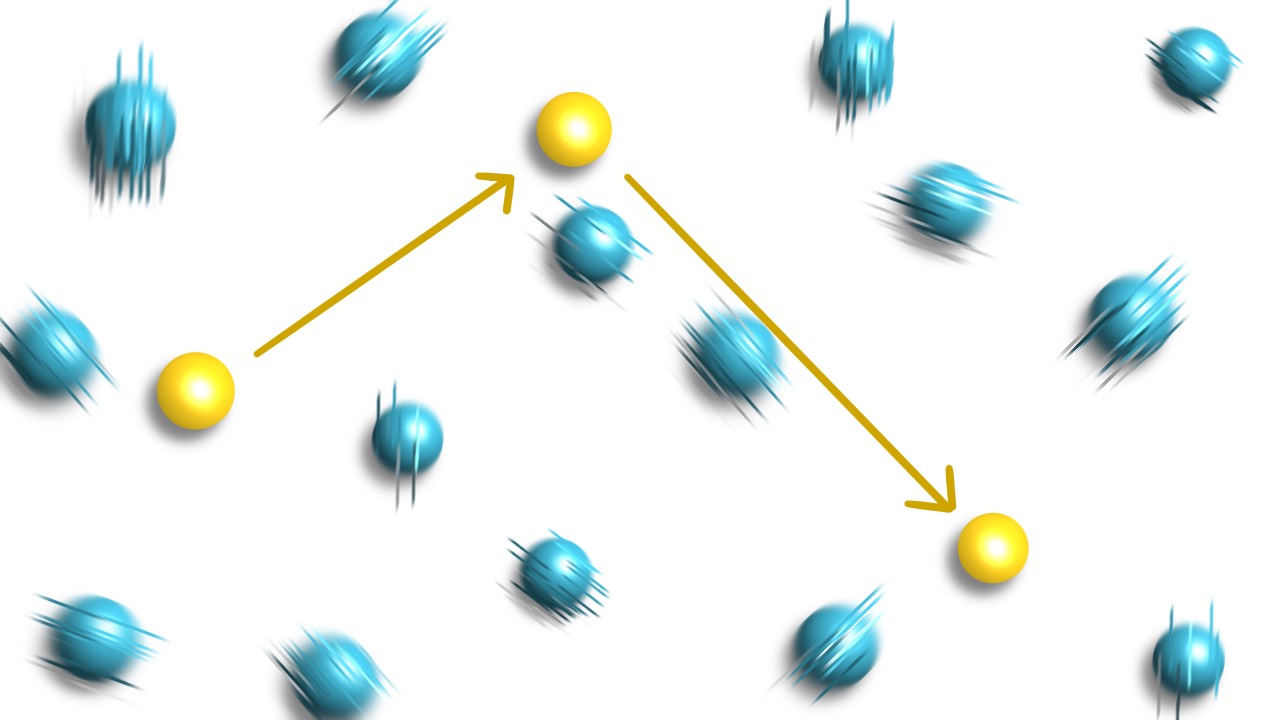
粒子の運動性は拡散係数と呼ばれる物理量で特徴付けられます. 拡散方程式の拡散係数です.多くの場合拡散係数は定数としますが, 高分子のような内部自由度がある系や,ガラスのような時空間的に不均一な系では拡散係数が時間的に揺らぐことが報告されています. そのような状況の中,仲井は内部自由度も時空間不均一性もない古典的な気体系でも拡散性の揺らぎが発現することを発見し, メカニズムと共に報告しました.
コンクリートはミクロに見るとかなり不均一な材料です. 一般に統計力学分野では,不均一系の拡散係数は時間と共に揺らぐことが知られています. コンクリート中の分子の拡散性も時間と共に変動すると考えなければいけないはずですが, これまで拡散性を一定と近似した解析しか実施されていない状況でした. この近似により,コンクリートの劣化寿命見積もりの精度が悪くなってしまう可能性があります. この状況に対し,名古屋大学の石田崇人 先生と共に, 揺らぐ拡散性を導入したコンクリート中の分子拡散のモデリングを行い報告しました.
一般に,粒子が複雑な拡散性を示す場合には,粒子を取り囲む流体の構造も複雑です. 仲井は,理想気体という最も構造が単純な流体中に粒子を導入して運動を計算したところ, ある状況下で粒子は拡散方程式では記述できない拡散(異常拡散かつ非ガウス拡散)を示すことを発見して報告しました.